Wheatstone Bridge Principle states the if four resistance P, Q, R and S are arranged to form a bridge as shown in figure with a cell E and one key K1 between the point A and C and galvanometer G and tapping key K2 between the points B and D, closing K1 first and K2 later on, if the galvanometer shows no deflection then bridge is balanced.
Current distribution in the circuit is shown in the figure. Total current by cell is I, it distributed to P and S as I1 and I-I1. Let current through galvanometer is Ig.
Current in Q is I1-Ig and in S current are I-I1+Ig. Resistance of galvanometer is G.
Now apply Kirchhoff’s 2nd law in ABDA, we get
I1P +Ig G – (I-I1) R=0 …..…1
Now apply Kirchhoff’s 2nd law in BCDB, we get
(I1 –Ig) Q – (I-I1+Ig) S – Ig G = 0 …….2
If value of R is such that the galvanometer shows no deflection that is Ig = 0. Putting this value in equation 1 and 2 we get
This last equation relating the four resistors is called the balance condition for the galvanometer to give zero or null deflection.
A practical device using this principle is called the meter bridge.


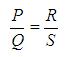
No comments:
Post a Comment